Circles, Percents, and Butter Cake

I was reminded of my grandmother's butter cake recipe today after seeing a math-related scenario (sort of a prompt) on the Math Forum, posted by Annie (whom I think I remember from college decades ago, but that's another story).

I love Gram's butter cake recipe (posted below) for several reasons. The recipe style reminds me of her (I can just hear her voice saying "Don't DUMP it in"); it's absolutely delicious; it's fun to make; and then there is this lovely warning: "This is too much batter for 2 9" pans." If you're a member of my family, that is code for "You probably want to make a 9", two-layer cake, so you're just going to have to eat some of the batter so it doesn't go to waste. Oh, DARN." (I should add here that you're eating raw eggs if you choose to do this, which is not advised, not to mention the gazillion calories. So let's consider this a hypothetical scenario that you're too smart to follow.)

So the question that always occurred to me, and which I have solved several times in my life, is: just how much excess batter are we talking about? If we fill two 9" round pans to the same depth to which we would have filled three 8" pans, what percentage of the batter do the cooks need to... um... dispose of?

I suppose if I pose this problem to students, I could come up with how many cupcakes a full recipe would make (probably about 30), then ask how many cupcakes you should make with the excess batter.

I just remembered: the frosting I always use for it also has interesting math. This was a recipe of my other grandmother's. It says to bring 2 tablespoons milk, 3 tablespoons butter, and 4 tablespoons of brown sugar to a boil, then stir in 1 1/2-2 cups of confectioner's sugar and a pinch of salt. But there's also a parenthetical note "or 3-4-5 proportions" under the 3 ingredients you boil. I used to entertain myself figuring out how much the options shifted the share of each ingredient.

By the way, although my frosting grandmother died about 20 years ago, Gram-of-the-butter-cake is still in fine form at age 93. If you live in Greensboro, NC, you've probably met her; it seems like everybody has!

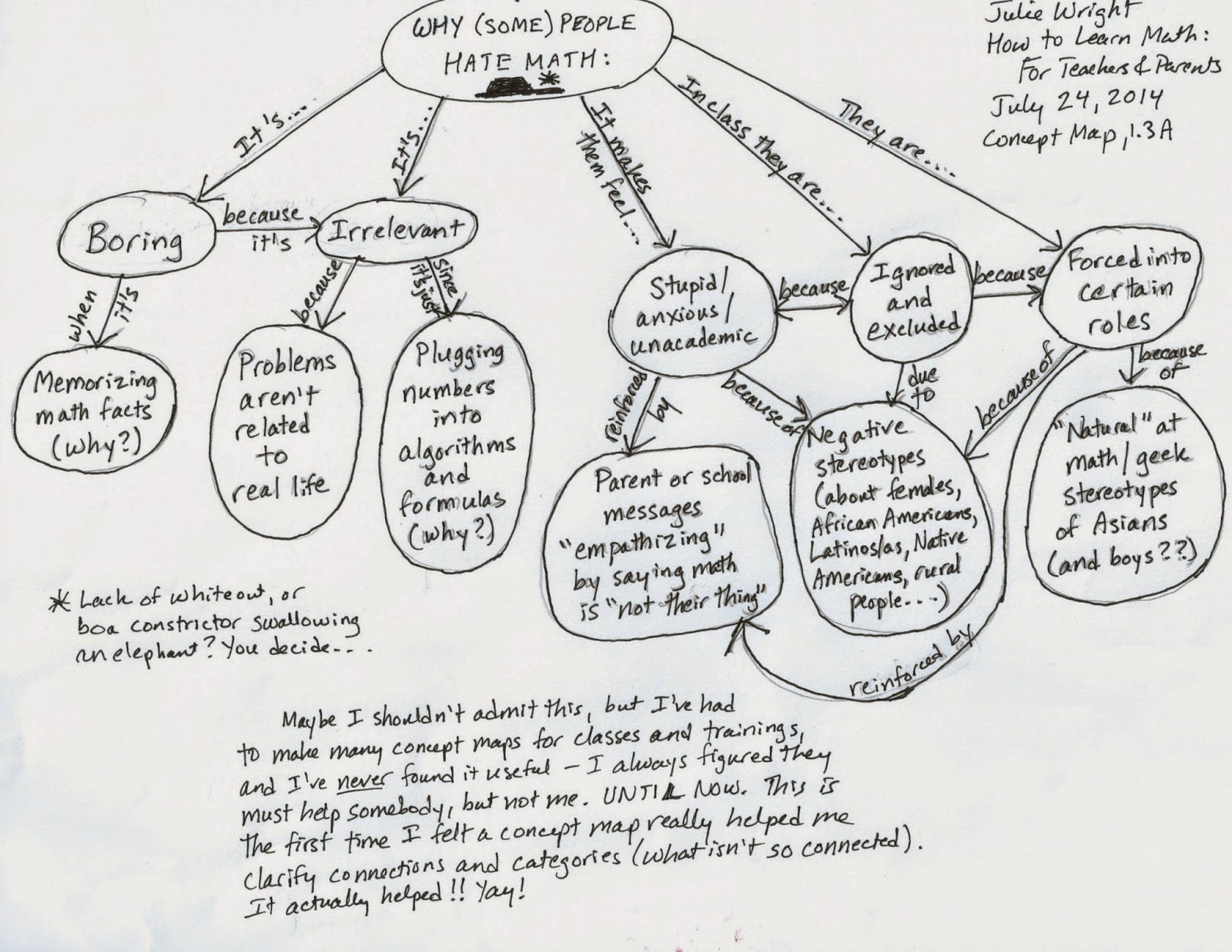
Why Do (Some) Students Hate Math?, or How I Learned To Love a Concept Map

This past summer, I took an incredibly good online course called How to Learn Math by Professor Jo Boaler at Stanford University. Its focus is on research on math learning and student mindsets that can transform students' experiences with math.

Near the beginning of the course, Jo Boaler and some of her students talked about some reasons why people often dislike math classes. As a response task, she asked us to summarize the reasons discussed with a concept map. I groaned, because although I am circumspect about sharing this view in education classes, I've despised concept maps ever since first trying one. I believed they must be useful for someone somewhere, so I've occasionally used them in teaching out of a sense of duty, but I consistently felt that rather than highlighting connections and promoting thought, they just resulted in a big muddled blob of words.

Nevertheless, I can comply with educational directives, so I gave it a whirl. To my astonishment, this concept map assignment actually clarified my thinking and made me see things in a new way. But before I get to that, here's the concept map in question:

Thanks partly to wonderful math education classes with Kasi Allen at Lewis & Clark, and partly to my own observations, none of these ideas were new to me, and I think about all of them a lot already. The breakthrough for me, though, was in seeing that the "boring/irrelevant" impressions of math and the "math is not for me because..." impressions of math are really two separate strands. Improving my teaching to address only one strand would help reach some students, but would leave others with their math hatred untouched. The interconnections in each strand might lead to a positive kind of snowball effect within that strand -- for instance, if I help students not to feel ignored and excluded in math because they belong to a certain group, their math anxiety will be reduced -- but to reach all math haters, I really need to make certain I am working on both strands.

If you want to comment, I'd love to know what you think about my concept math epiphany or what you feel is missing from the reasons students hate math. I was surprised they didn't talk about standardized tests or about the feeling that in math answers are right or wrong without any gray areas (an impression some people find reassuring but many find terrifying), but since they didn't, I left it out of my concept map assignment.

Typed, Targeted Feedback on Student Papers: How To Do It

As a grizzled veteran of the MathTwitterBlogosphere of, let's see, about 5 weeks, I've already seen several really inspiring conversations among teachers (including @davidwees, @k8nowak, @occam98, @cheesemonkeysf, @fawnpnguyen, @absvalteaching, and @TRegPhysics) who are searching for a good way to achieve all of these things at once:

• provide high-quality written feedback on student papers (especially, feedback separate from or instead of scores and grades, since research shows students will only read the grades if both are there)
• avoid repeatedly handwriting the same comments
• have the comments personalized and right beside the work being commented upon
• provide each student (and family?) with an online, commented document instead of or in addition to a physical paper
• do all this without installing expensive software (sometimes, without third-party software at all)
• do all this in a reasonable amount of time and without losing one's sanity

So, here's the best procedure I've come up with so far. If anyone wants to comment and suggest improvements, I'll fold your ideas in, crediting you. 

1. Make a test that has room reserved for your comments: a column to the right or left of the problems, a box under each problem or at the bottom of the page, whatever. Make sure to instruct students not to write in that area. (idea from Trevor Register, whose blog post was passed on by John Burk) 
2. After students take the test, arrange their papers in your class list order (presumably alphabetical). You may want to include blank pages for absent students. Scan the tests into a pdf file. (I'm assuming most of us have access to photocopiers that can do this quickly, but sometimes teachers don't realize it can be done. Ask around if you're not sure!)
3. If you have a Mac, open the pdf file using Preview. (If you have a PC, you'll need some other procedure for steps 3 & 4; I'll add it if someone suggests one.) Add your comments using the Tools/Annotate/Text option: click and drag to make a box to type your text in, and type it in. You can change the color, font, and size for the text box; sadly, you can't do equations. 
4. For your next comment, you don't need to select Tools/Annotate/Text again, just make a new box. If you want to reuse a comment, click on it and copy it, then just paste it in on the next student's paper. When you've finished commenting, save the pdf.
   Here's an example I made using real test questions (leaving out the hardest) and real student work (copied over in my handwriting for privacy reasons). See especially how the comment for #5 is almost identical on the two papers -- no copying by hand, though!!
5. Now you can split the pdf with everyone's papers into individual papers. You can use the free website splitpdf.com for this (found by John Burk). Select the file you are splitting, and use the page range thing (if needed; you'll also use "More+") and "Customize split files' names" to (for example) save student JW's test to jw.pdf. (Entering individual file names is a bit painful; anyone have improvements to suggest?) (splitpdf.com also offers a free Chrome "app," but as far as I can tell that just takes you to their web page. John also found PDFsam, which might be even more powerful but needs to be installed and uses Java.)
6. When you hit "Split!", it will make a .zip file and ask you where on your computer to put it. When you unzip the file, it will make a directory with the student papers stored in it. If you want to, you can then upload the whole directory at once to Google Drive, as I did for my split, commented sample test. 
7. The biggest problem I see is, now how do I share the papers out with the students? Presumably each student could have a directory that they have permissions for and others don't, but shoving each file into the appropriate directory would be a pain. Any thoughts, especially from anyone who's been working with Google Classroom?

Conclusion so far: I would rather do this procedure than write comments on tests by hand. I'd especially like to use it to give students a chance to work more on their papers BEFORE getting the scores/grades. (I would still give highest points to students who did high-quality work in the first round, but I'd give generous partial credit for changes made after my comments.) However, I would like a better way to customize the file names in step 5 and (especially) to painlessly redistribute the commented student papers into appropriate directories where they could access them (step 7).

PS Can you guys actually see the sample files mentioned in Steps 4 & 6? The permissions on the directory, and therefore the files, are supposed to be set so you can, but I'm not sure it's working.